This article first appeared in Data Science Briefings, the DataMiningApps newsletter. Subscribe now for free if you want to be the first to receive our feature articles, or follow us @DataMiningApps. Do you also wish to contribute to Data Science Briefings? Shoot us an e-mail over at briefings@dataminingapps.com and let’s get in touch!
Contributed by: Bart Baesens, Véronique Van Vlasselaer
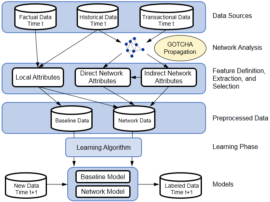
In what follows, we would like to discuss a brief case study from research that we did. More specifically, it concerns the GOTCHA! fraud detection tool for social security fraud. You can see the architecture of Gotcha below.
It starts with three types of data sources: factual data, historical data, and transactional data. These are then used to derive both local and network attributes. Direct network attributes are based on featurizing the egonet, whereas indirect network attributes originate from the PageRank algorithm. The combined data is analyzed by a learning algorithm to build a predictive model. The resulting analytical model can then be used to label new observations. We used GOTCHA! for both Social Security and credit card fraud detection.
Let’s first zoom into the data sources. Factual data represents local data characterizing the current state of the subject. In Social Security fraud, this is the current state of the company, such as its sector, age, financial statement data, and so on. In credit card fraud, this can be the current state of the credit card holder measured by his demographics, bank statements, and so on, or the current state of the merchant measured by his store address, income, and other characteristics. Historical data represents the behavioral changes of the subject. Examples are changes in legal form, sector, or demographics. Transactional data represents interactions between subjects. Examples are companies that share the same address, work place, employees, and similar characteristics; or credit card transactions between credit card holders and merchants.
For Social Security fraud, the network was constructed by connecting companies based on shared resources such as employees, equipment, and physical address. The goal here was to find those companies that intentionally do not contribute Social Security to the government and go bankrupt. For credit card transaction fraud, the network was constructed by connecting people to stores based on where they make their purchases. The goal here is to find those transactions that are likely to be fraudulent because they were made with stolen or copied credit cards.
Here you can see the performance of GOTCHA! for Social Security fraud. It is measured by the area under the receiver operating characteristic curve.
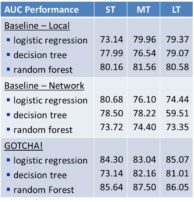
Three prediction windows are used: short term (which is six months), medium term (which is 12 months), and long term (which is 24 months). We used three classification techniques: logistic regression, decision trees, and random forests. From the table, you can see that the GOTCHA! model with random forests gives the best performance on the combined local and network attributes. We did not find any significant interaction between the local and network attributes. GOTCHA! also performed very well in out-of-time validation.
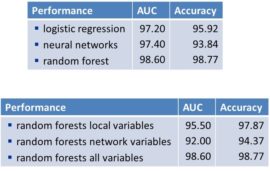
Here you can see the performance of GOTCHA! for credit card fraud detection.
The first table depicts the area under the ROC curve (or AUC) and the classification accuracy measured by the percentage of correctly classified observations. Both measures are reported for logistic regression, neural networks, and random forests. It can be seen that random forests give the best overall performance with an AUC of 98.60% and an accuracy of 98.77%. Note that this is an exceptionally high performance, indicating that credit card fraud can be well predicted. The second table contrasts the performance of the local and the network variables using random forests. The local variables included operationalizations of the RFM (or recency, frequency and monetary constructs), complemented with demographic information about the transaction. Again, it can be seen that the best performance is obtained by using a combination of local and network variables.