Recommender Systems with Multiple Types of Feedback

Traditionally, recommender systems are evaluated on one metric, however, it is often desirable that the recommender system also scores well on other metrics. This article describes a couple of approaches for dealing with this problem. We specifically zoom in on the paper published at the most recent KDD conference, “An Empirical Study on Recommendation with Multiple Types of Feedback” by Tang, Long, Chen and Agarwal from LinkedIn.

When building recommender systems, we normally try to optimize one metric. Something like the accuracy of the model, the precision at K or the recall, or the F1-score (which is the harmonic mean of precision and recall), or we build a ROC curve to calculate and compare the AUC of different models. These are all valid metrics for evaluating recommender systems, and each has its own merits. Those listed here all focus on identifying the items the user will perform an action on (adding an item to basket in an ecommerce setting, clicking on a web search result, choosing which article to read on a news website, or selecting a video to watch on a video provider).

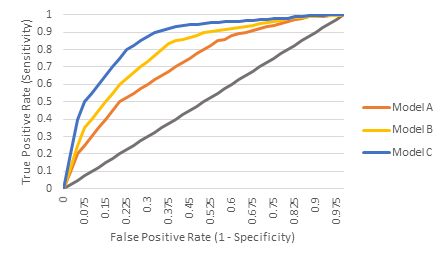
Figure 1: typical ROC curves to compare several recommender systems’ performance on one metric.

In the case where we only look at one metric, it is not such a hard problem to select which model performs best. For example, we just select the model with the highest AUC in Figure 1, which in this example is Model C.

However, many systems nowadays allow users to provide other types of feedback, limiting the approach of using only one metric to evaluate the system on. Tang et al. [4] give the example of email campaigns: When a user receives promotional emails from a company, the user can perform different actions: he or she can choose to click on links in the email to further engage with the content, or can also unsubscribe from all emails from the company or label the email as spam. Another example from [4] is based on a social media feed, where updates can not only be clicked on, but updates from a specific source can also be hidden. These types of additional feedback potentially provide extra information for the recommendation models, and can be taken into account when building the recommendation system to achieve better results.

Sometimes we want to take into account other aspects when drafting the top items to recommend, such as serendipity, novelty, diversity, trust, and so on. This seems advisable, as previous research has shown that user satisfaction does not always correlate with high recommender accuracy [1].

In the recent paper presented at KDD based on an empirical study within LinkedIn [4], three methods were proposed to deal with this problem. They are:

1. Combine the different models: train one model for each type of feedback then combine the models into a single model. This is only feasible if the separate model formulations are the same.
2. Sequential training based on Bayesian inference: train one model on one type of feedback, then use that model as a prior to train the next model. This method takes the trained results from the previous model to regularize the next model’s fitting. Unfortunately, there are some assumptions to this method, which are not always fulfilled in reality (see the paper for more information).
3. Joint training, where multiple types of feedback are put into a single training problem. Still only one type of feedback needs to be optimized, but the other types of feedback can be incorporated in the training problem as constraints.

In the paper presented at KDD, the three methods are empirically tested both in an offline and online context. The joint training method with using constraints achieves the best results, closely followed by the model combination approach.

When optimizing for two types of feedback (≈ two objectives), the results of these methods can be represented visually:

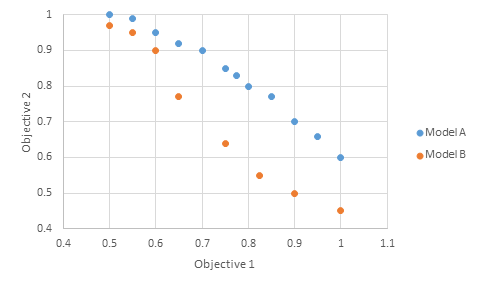
Figure 2: Visually representing the performance trade-off between two recommender systems.

In the small example in Figure 2, we can see that if we look at the performance of model A and B and consider two objectives (achieving multiple results for varying the model’s parameters), Model A dominates Model B.

These three proposed methods are closely linked to the research on multi-objective optimization, which has been extensively studied in the operations research literature. The following approaches, further discussed in [3], are used to address multi-objective optimization problems, and can be applied to recommender systems too. We can (1) try to find Pareto optimal solutions, (2) to take a linear combination of the multiple objectives and reduce the problem to a single-criterion optimization problem, (3) optimize only the most important criterion and convert the other criteria to constraints, and (4) consecutively optimizing one criterion at a time, converting an optimal solution to constraints and repeating the process for other criteria. Note that approach (2) is similar to the model combination approach discussed above, (3) is similar to the joint training approach, and (4) is similar to the sequential training approach presented in the paper by Tang et al. [4].

Another approach is to combine multiple recommender systems in one hybrid system. Hybrid recommender strategies are the combination of two different families of algorithms, namely content-based and collaborative filtering [2]. These hybridization strategies can be both single-objective or multi-objective. Examples of these strategies are weighted approaches, voting mechanisms between the different algorithms, switching between different recommenders, or re-ranking the results of one with another recommender system.

In practice, LinkedIn implemented the model combination approach, because it is easier to train. This method needs to only train two individual models and then vary the weights to obtain various tradeoffs between the multiple types of feedback. The joint optimization approach requires to retrain the joint model for each of the weight parameters.

Conclusions:

• This article discussed doing recommendation with multiple types of feedback.
• Multiple objectives are often desirable in recommender systems.
• The area of recommender systems can learn from the domain of operations research for multi-objective optimization approaches and methods.
• Three approaches were presented of which one is currently implemented in LinkedIn.

References:

• [1] Adomavicius, G. and Youngok K. (2015), “Multi-Criteria Recommender Systems,” Recommender Systems Handbook, Second Edition, p. 847–80.
• [2] Ribeiro, M., Lacerda, A., Veloso, A., and Ziviani, N. (2012), “Pareto-Efficient Hybridization for Multi-Objective Recommender Systems,” in RecSys ’12, p. 19-26.
• [3] Adomavicius, G. and Tuzhilin, A. (2005), “Toward the next generation of recommender systems: A Survey of the State-of-the-art and Possible Extensions”, IEEE Transactions on Knowledge and Data Engineering, 17(6), p. 734-769.
• [4] Tang, L., Long, B., Chen, B., and Agarwal, B. (2016), “An Empirical Study on Recommendation with Multiple Types of Feedback,” in Proceedings of KDD ’16.