Check Mate? The Current State of Board Game AI

Go is considered to be the most complex game humans play. The recent news of Google’s Go Artificial Intelligence (AI), AlphaGo (http://deepmind.com/alpha-go.html), defeating reigning European Go champion Fan Hui with a whopping 5-0 and world champion Lee Sedol after an incredible 4-1 match has put board game AI back in the spotlight. Remarkable is that this technological accomplishment was expected to be several decades away from being possible. In this short article we will discuss why board game AI is actively being researched, why AlphaGo defeating expert Go players is impressive and earlier than expected, and what challenges still lie ahead for the board game AI research community.

Why do we care about board game AI?

Since the 1950’s AI researchers have been developing algorithms that allow computer programs to play board games. John Von Neumann’s theory around the minimax algorithm and Claude Shannon’s paper “Programming a Computer for Playing Chess” are generally considered the main starting points for board game AI research. Since then, tremendous work has been done around developing AIs for games such as chess, checkers, backgammon, Go and others. AI researchers were eager to test how capable machines could be of performing tasks that require what people at the time considered extraordinary human intelligence. Board games such as chess and Go were (are) excellent candidates for such research: experts in these games are considered to be highly intelligent beings in possession of extremely developed reasoning capabilities, and board game rules and set-up are simple enough for researchers to create a controlled environment.

Fundamentals of board game AI

In order to understand what makes developing board game AIs so complex we first have to introduce the concept of a game tree. A game tree of a specific game is a tree-representation of all possible games that can be played following the rules of the game. The root of the tree is the start configuration of the game (e.g. for Go this is an empty board, for chess this is the board situation before the first player makes his first move, etc.). The leaf nodes of the tree represent all the possible endings of the game (e.g. in chess these are all the possible checkmate and remise positions). Every other node in the tree corresponds to board positions that could possible occur during a game. Figure 1 depicts the game tree of the first 3 steps of the game Tic Tac Toe. The root node is an empty grid. The following row of board positions contains the results of all the legal moves the first player can perform, followed by the board positions the second player can reach, etc. (symmetrical board positions have been omitted from the tree). Note that already after 2 steps in this rather simplistic game the game tree becomes too large to easily represent visually. In fact, the whole tree would consist of 5,748 nodes without symmetry breaking and 765 nodes if we removed all symmetrical board positions.

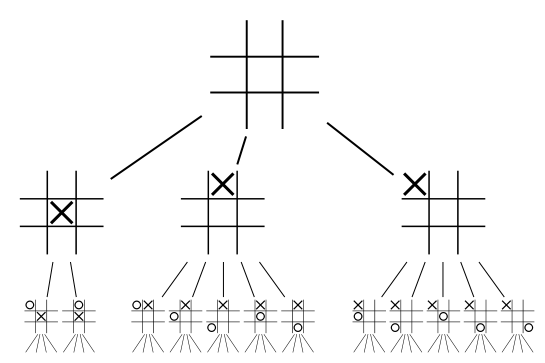Figure 1: Game tree of the first 3 steps of tic-tac-toe. Symmetrical board positions have been omitted. Image source: https://en.wikipedia.org/wiki/File:Tic-tac-toe-game-tree.svg

Game trees are of great importance to game AIs, and most algorithms are heavily reliant on them. Once a whole game tree is constructed, a simple algorithm can be created that traverses the tree from the current game position all the way to the leaf nodes to analyse which next move will most likely lead to a winning board position. The minimax algorithm (Wikipedia) works like this, and is the basis for most board game AIs. This approach is fine for simpler games such as tic-tac-toe, but for more complex games in which more moves are possible in each turn and with a larger game length it becomes infeasible to 1) construct the whole game tree in memory or 2) traverse the current board position all the way down to each reachable leaf node. For example: The full checkers tree has around 10^20 (or 100,000,000,000,000,000,000) nodes, the full chess tree around 10^47 nodes, and the Go tree around 10^170 nodes! It is easy to see that for game trees this large the simplistic strategy sketched above would require infeasible amounts of memory and computing time.

For these complex games, optimizations to the minimax algorithm have been proposed that improve on the memory- and time-requirements of finding a good next move. The optimizations generally revolve around 1) not having to visit all branches of a search tree and 2) not having to search through a branch all the way to the leaf nodes. In what follows we will mention some of the more impactful optimizations, and how the AlphaGo algorithm uses them.

Alpha-beta pruning (Wikipedia) is an algorithm that allows for the cutting of branches from the game tree that would lead to a result worse than previously examined moves. This type of pruning causes an improvement in runtime without sacrificing optimality.

Monte Carlo tree search (Wikipedia) is a sampling technique in which a number of random games are played starting from the current position, and the move that on average resulted in the best result (the most games won) is selected for the next step. Note that using Monte Carlo tree search to determine your next move could lead to non-optimal move selection.

A last optimization technique over having to evaluate the whole game tree we will discuss is assigning a score to each board position, indicating how favorable a position is. Assigning a score to leaf nodes is trivial: a win should get a high (maximal) score, a loss a low (minimal) score and a tie a neutral score. However for non-leaf nodes it can be very challenging to determine how (un)favorable a specific board position is. A (naive) example of scoring chess board positions is to give positive scores to board positions in which you have more pieces remaining than the opponent, and a negative score if vice versa. This scoring mechanism has of course many flaws (e.g. in chess, a pawn is almost always less valuable than a queen, but not always, depending on the position of the piece.) but nicely shows why assigning board position scores can be extremely difficult for complex games. Once a good board-scoring method is chosen, the algorithm can traverse the tree several turns deep, and evaluate which next move results in the best board-score further down the line. The deeper the program looks in the game tree, the better the move selection will be, but the higher the memory and runtime requirements. To give you an idea: the deep blue chess computer from IBM was the first chess program to ever beat a world champion, and would generally look 6-20 moves deep in the tree while being constrained to standard chess tournament time controls. Traditionally board-scoring functions would be optimized by letting the game AI play slightly modified versions of itself, constantly discarding inferior AIs and focussing on optimizing superior AIs. This way game AIs can learn by playing millions of games against itself, something unfeasible for humans.

AlphaGo: deep learning meets minimax

A big part of the success of Google’s AlphaGo Go AI can be accredited to combining the aforementioned optimization techniques with current deep learning breakthroughs. Fundamental to AlphaGo is the artificial neural networks used to score Go board positions. These neural networks are trained based on a corpus of millions of self-play and human-play games, allowing them to learn which positions are favorable, and which are not. Because of the complexity of Go (a 19×19 board with 3 possible states for each tile) scoring a Go board position is (or: was?) something considered to be a highly intuitive affair, and extremely complex. It is because of this complexity that the AI community expected that technology would still need decades in order to evolve before being able to make such “intuitive” assessments in face of such a massive game tree.
Besides using deep learning for board position evaluation, AlphaGo also used neural networks for the selection of branches to inspect further, as well as monte carlo tree search. For the full functionality of AlphaGo, we refer to the corresponding paper referenced at the end of this article.

The future of board game AI

What does the future hold for the board game AI community? Given AlphaGo’s victory over reigning Go world champion Lee Sedol, we as humans might have to acknowledge machines to be superior in even the most complex and intuitive game played by humans.

However, still today, the game of Go cannot be considered solved in the strict definition of the term. One of the interesting questions still unanswered about Go (and also about chess for that matter) is if perfect play on both sides would result in a win for the first player, a win for the second player, or a tie. Answering this question would ultra-weakly solve this game and is interesting to assess the “fairness” and reason about the abstract properties of the game. Famous examples of (at least) ultra-weakly solved games are Connect Four (in case of perfect play on both sides the first player wins) and Checkers (with the proof showing that in case of perfect play checkers results in a draw required a legendary 18 years of computation).

Even though we, humans, are slowly but surely being outclassed by machines in even the most complex of games, board game AI is far from being solved. For instance, Stratego and Connect6 are still hard games for computers to do well at… perhaps a next challenge for the DeepMind team?

References

• Claude E. Shannon. Programming a Computer for Playing Chess. Philosophical Magazine, 41(314):256-275, 1950.URL: http://vision.unipv.it/IA1/ProgrammingaComputerforPlayingChess.pdf.
• M. Robson (1983). “The complexity of Go”. Information Processing; Proceedings of IFIP Congress. pp. 413–417.
• Silver, D., Huang, A., Maddison, C. J., Guez, A., Sifre, L., van den Driessche, G., … & Dieleman, S. (2016). Mastering the game of Go with deep neural networks and tree search. Nature, 529(7587), 484-489.